讲座题目:Explicit Numerical Approximations for Nonlinear Stochastic Differential Equations
主办单位:3522vip浦京集团官网
报告专家:李晓月(东北师范大学 教授)
报告时间:2021年6月2(周三) 15:00-16:00
腾讯会议ID:148 796 480
会议链接: https://meeting.tencent.com/s/imo7GpeqFFBz
专家简介:李晓月,东北师范大学数学与统计学院教授,博士生导师,美国数学会评论员。长期从事随机微分方程稳定性理论、应用及数值逼近的研究, 发表SCI检索论文30余篇,单篇引用率达200余次,部分成果发表在SIAM J. Numer. Anal.、 SIAM J. Appl. Math.、IMA J. Numer. Anal.、J. Differential Equations 等学术期刊上。主持过国家自然科学基金项目和省部级项目多项。
摘要:Solving stochastic differential equations (SDEs) numerically, explicit Euler-Maruyama (EM) schemes are used most frequently under global Lipschitz conditions for both drift and diffusion coefficients. In contrast, without imposing the global Lipschitz conditions, implicit schemes are often used for SDEs but require additional computational effort; along another line, tamed EM schemes and truncated EM schemes have been developed recently. Taking advantages of being explicit and easily implementable, truncated EM schemes are proposed in this paper. Convergence of the numerical algorithms is studied, and 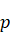 th moment boundedness is obtained. Furthermore, asymptotic properties of the numerical solutions such as the exponential stability in
th moment boundedness is obtained. Furthermore, asymptotic properties of the numerical solutions such as the exponential stability in 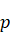 th moment and stability in distribution are examined. Several examples are given to illustrate our findings.
th moment and stability in distribution are examined. Several examples are given to illustrate our findings.